BASBLib - A Library of Bilevel Test Problems

A growing collection of bilevel problems

b_1991_01 : Linear-Linear problem from [Bard, 1991]:

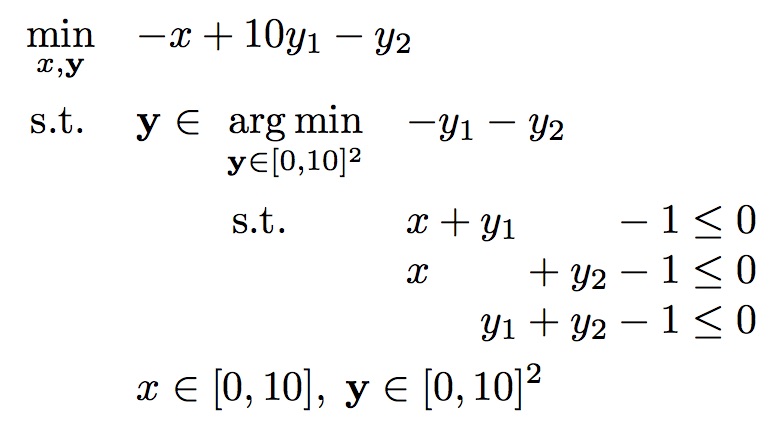
Comments on the problem

First, let us note that our formulation is based on the original source (Bard, 1991), i.e., the first constraint is x + y1 - 1 <= 0 whereas in the further sources it was changed into x - y1 - 1 <= 0. However, this does not have an impact on the optimal solution.

Moreover, in (Bard, 1998) & (Shimizu et al., 1997) wrong minimum value of outer-objective F* = 1.0 is reported, which actually is F* = -1.0.

The leader is faced with an ambiguous situation for all choices but one. Only at x = 1 is the follower’s response, y = (0.000, 0.000), unique. For 0 <= x < 1, F* = -1.0 is realized only when the follower cooperates and picks the largest possible value for y2, such that x + y2 = 1. Finally, note, that x = 0, y = (0.000, 1.000) is the best outcome from the follower’s perspective f* = -1.0, while keeping the same mimum value F* = -1.0 for the leader.

Optimal solution

Objective values Solution points
F* = -1.000 x* = 1.000
f* = 0.000 y* = (0.000, 0.000)

Sources where this problem occurs

Original source:

Other sources:

Description of the problem in the AMPL format

var x >= 0, <= 10;         # Outer variable
var y{1..2} >= 0, <= 10;   # Inner variable
var l{1..7} >= 0, <= 10;   # KKT Multipliers

minimize outer_obj: -x + 10*y[1] - y[2];  # Outer objective

subject to
# Inner objective:
    inner_obj: -y[1] - y[2] = 0;
# Inner constraints
    inner_con1:     x + y[1] - 1 <= 0;
    inner_con2:     x + y[2] - 1 <= 0;
    inner_con3:     y[1] + y[2] - 1 <= 0;
# KKT conditions:
    stationarity_1:    -1 + l[1] + l[3] - l[4] + l[5] = 0;
    stationarity_2:    -1 + l[2] + l[3] - l[6] + l[7] = 0;
    complementarity_1: l[1]*(x + y[1] - 1) = 0;
    complementarity_2: l[2]*(x + y[2] - 1) = 0;
    complementarity_3: l[3]*(y[1] + y[2] - 1) = 0;
    complementarity_4: l[4]*y[1] = 0;
    complementarity_5: l[5]*(y[1] - 10) = 0;
    complementarity_6: l[6]*y[2] = 0;
    complementarity_7: l[7]*(y[2] - 10) = 0;

References