BASBLib - A Library of Bilevel Test Problems

A growing collection of bilevel problems

sib_1997_02 : Linear-Linear problem from (Shimizu et al., 1997):

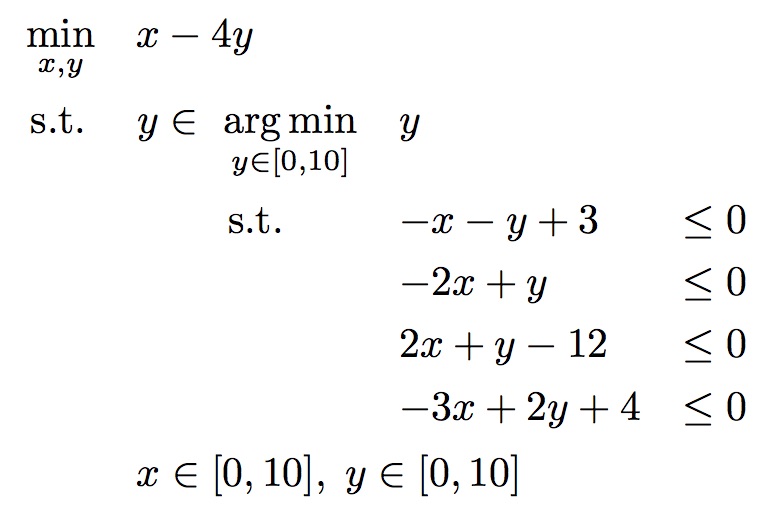
Comments on the problem

In all sources mentioned below, the reported optimal solution occurs at (x, y) = (4.0, 4.0) with F* = -12.0 and f* = 4.0. However, it is easy to check that this point is not bilevel feasible. When the leader (outer decision maker) selects x = 4.0, the follower (inner decision maker) will respond with y = 0.0. This is better for the follower, but not for the leader.

Moreover, graphical analysis in Figure 16.1.1 in (Shimizu et al., 1997) shows discrepancy between geometry (polyhedron depicting constrain region) and the problem formulation. Therefore, in sib_1997_02v we present a variation of this problem. The only difference is the fourth inner constraint, which is changed from -3x + 2y + 4 <= 0 into 3x - 2y - 4 <= 0. After this modification, the optimal solution occurs at (4.0, 4.0) with F* = -12.0 and f* = 4.0.

Optimal solution

Objective values Solution point
F* = -2.000 x* = 2.000
f* = 1.000 y* = 1.000

Illustration of the problem

Outer Problem Inner Problem

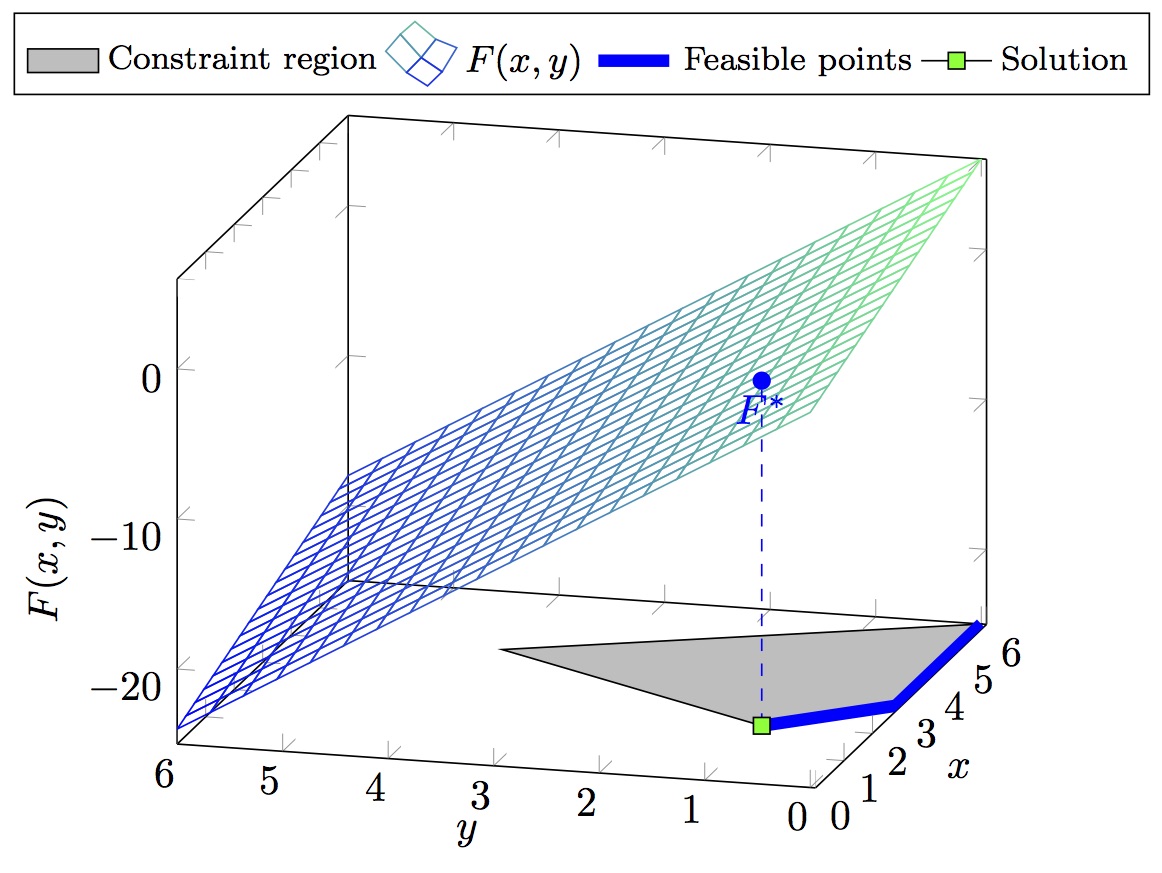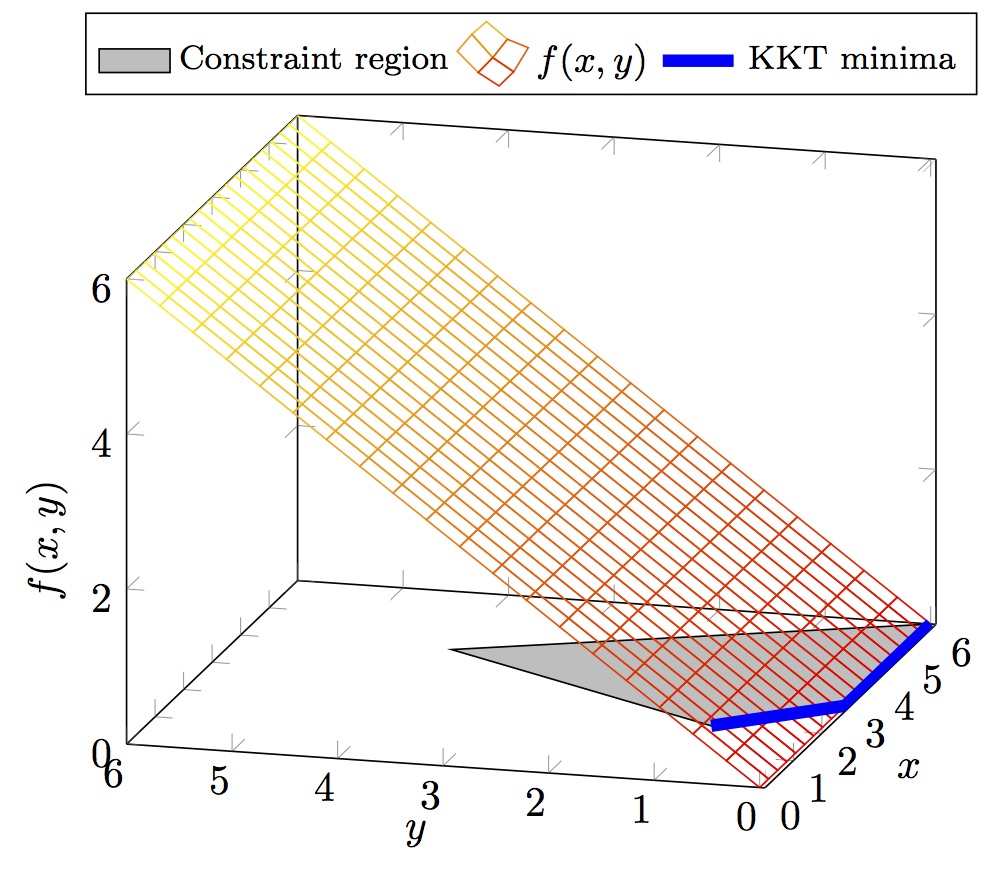Sources where this problem occur

Original source:

Other sources:

Description of the problem in the AMPL format

var x >= 0, <= 10;         # Outer variable
var y >= 0, <= 10;         # Inner variable
var l{1..6} >= 0, <= 10;   # KKT Multipliers

minimize outer_obj: x - 4*y;  # Outer objective

subject to
# Inner objective:
    inner_obj: y = 0;
# Inner constraints
    inner_con1: -x - y + 3 <= 0;
    inner_con2: -2*x + y <= 0;
    inner_con3: 2*x + y - 12 <= 0;
    inner_con4: -3*x + 2*y + 4 <= 0;
# KKT conditions:
    stationarity:      1 - l[1] + l[2] + l[3] + 2*l[4] - l[5] + l[6] = 0;
    complementarity_1: l[1]*(-x - y + 3) = 0;
    complementarity_2: l[2]*(-2*x + y) = 0;
    complementarity_3: l[3]*(2*x + y - 12) = 0;
    complementarity_4: l[4]*(-3*x + 2*y + 4) = 0;
    complementarity_5: l[5]*y = 0;
    complementarity_6: l[6]*(y - 10) = 0;

References