BASBLib - A Library of Bilevel Test Problems

A growing collection of bilevel problems

Quadratic-Nonlinear bilevel problem from [Mitsos & Barton, 2007]

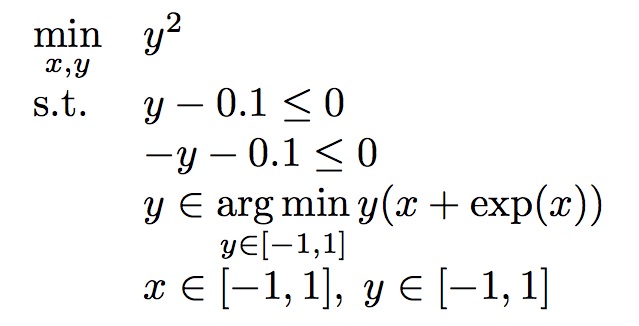
Optimal solution

Objective values Solution point(s)
F* = 0.000 x* = -0.567
f* = 0.000 y* = 0.000

Has unique optimal solution point (x, y) = (-0.567, 0) with an objective values: F* = 0.0 and f* = 0.0.

Illustration of the problem

Outer Problem Inner Problem

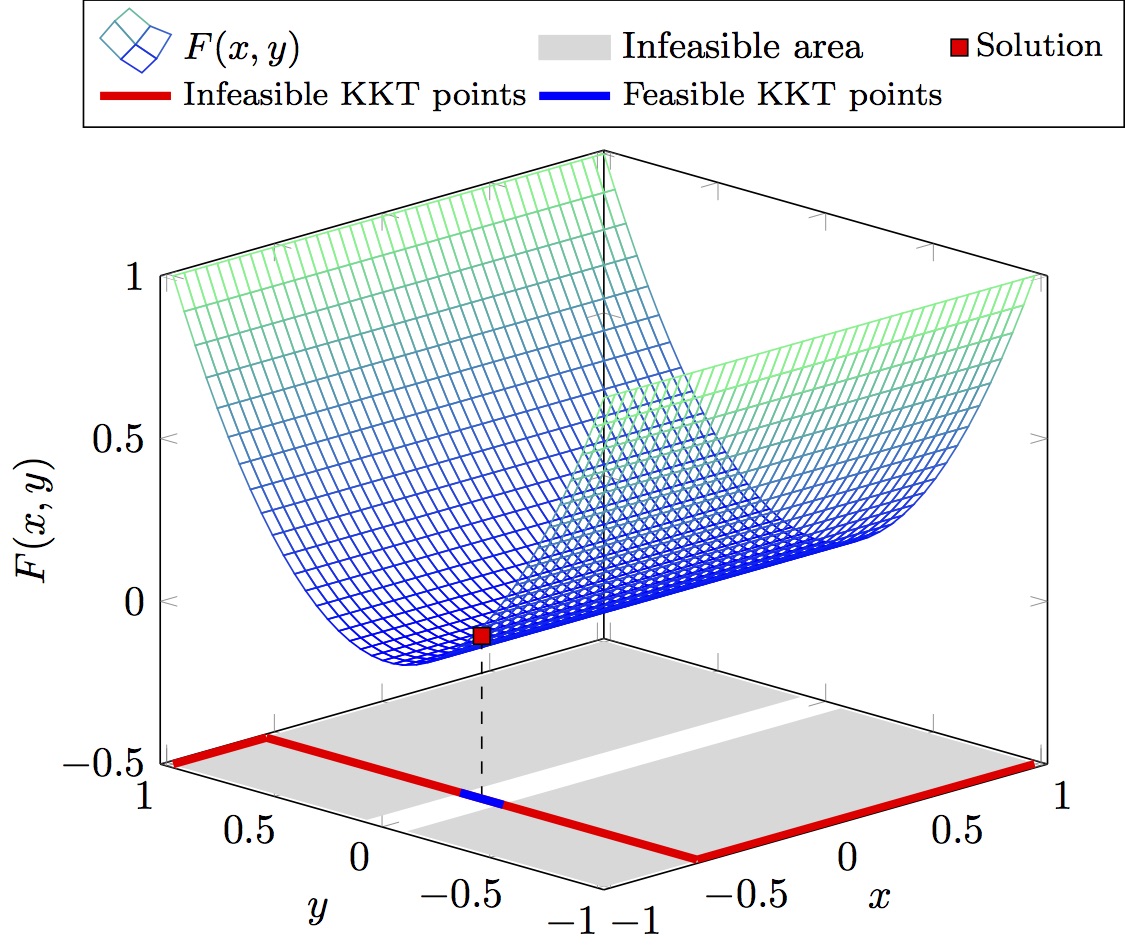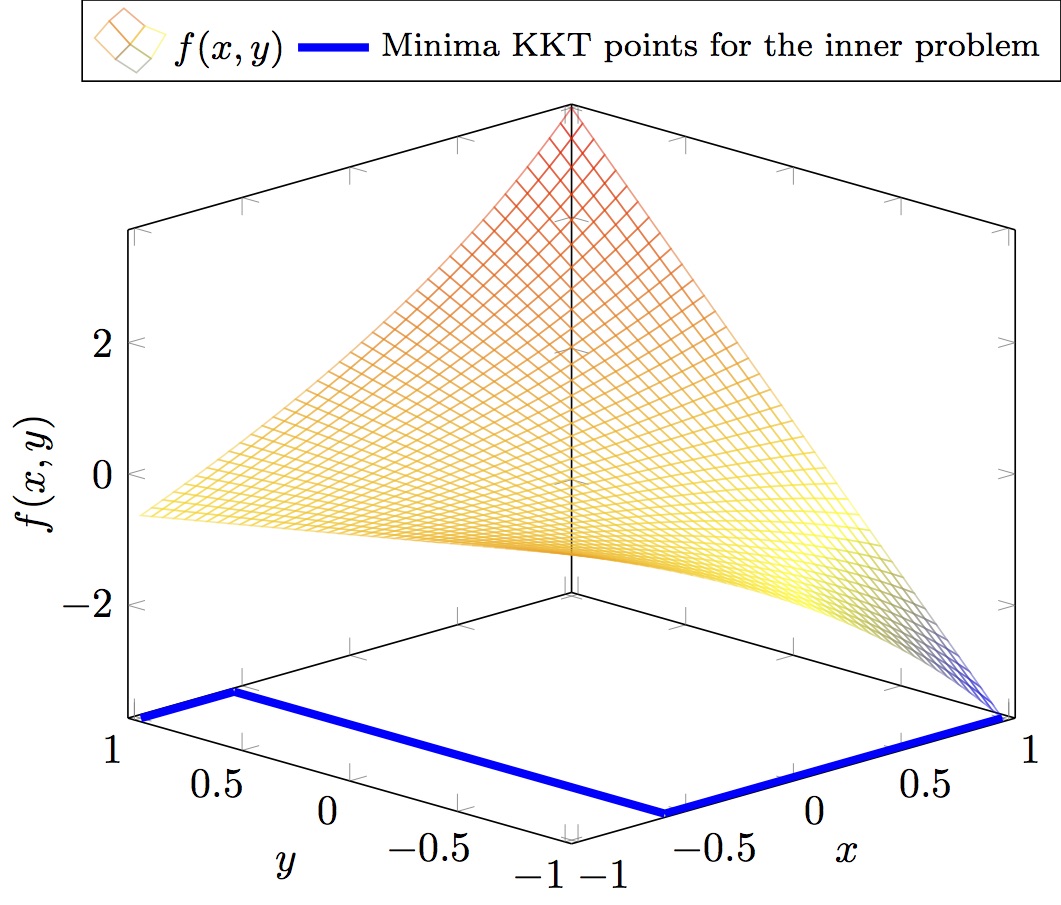Description in the AMPL format

var x >= -1, <= 1;          # Outer variables
var y >= -1, <= 1;          # Inner variables
var l{1..2} >= 0, <= 5;     # KKT Multipliers

minimize outer_obj: (x-x)^2 + y^2;  # Outer objective

subject to
# Outer constraints:
    outer_con1:  y <= 0.1;
    outer_con2: -y <= 0.1;
# Inner objective:
    inner_obj: x*y + exp(x)*y = 0;
# KKT conditions:
    stationarity:      x + exp(x) - l[1] + l[2] = 0;
    complementarity_1: l[1]*(-1 - y) = 0;
    complementarity_2: l[2]*(y - 1) = 0;

References