mb_2007_22v : Quadratic-Nonlinear bilevel problem from [Mitsos & Barton, 2007]
Comments on the problem
This is a variation of mb_2007_22 problem. The only difference is the outer objective function, which is changed from (x - 0.6)^2 + y^2 to (x + 0.6)^2 + y^2.
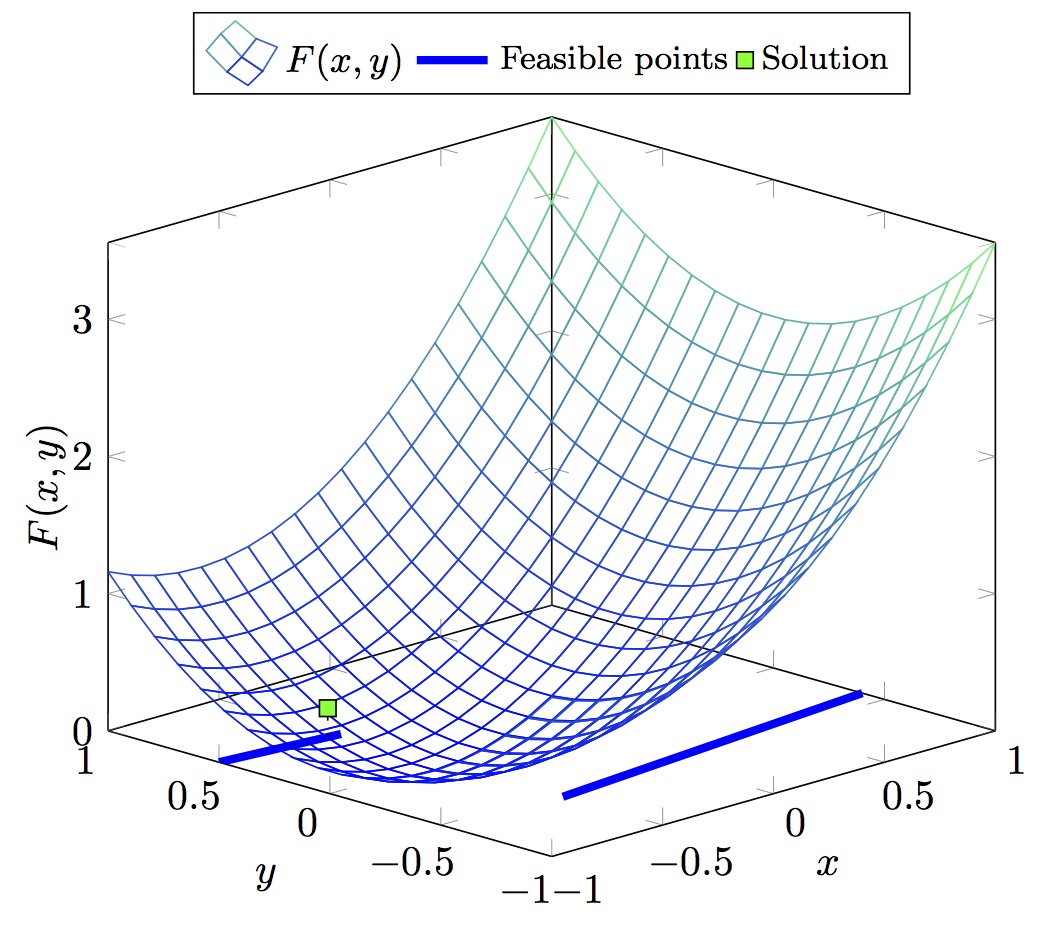
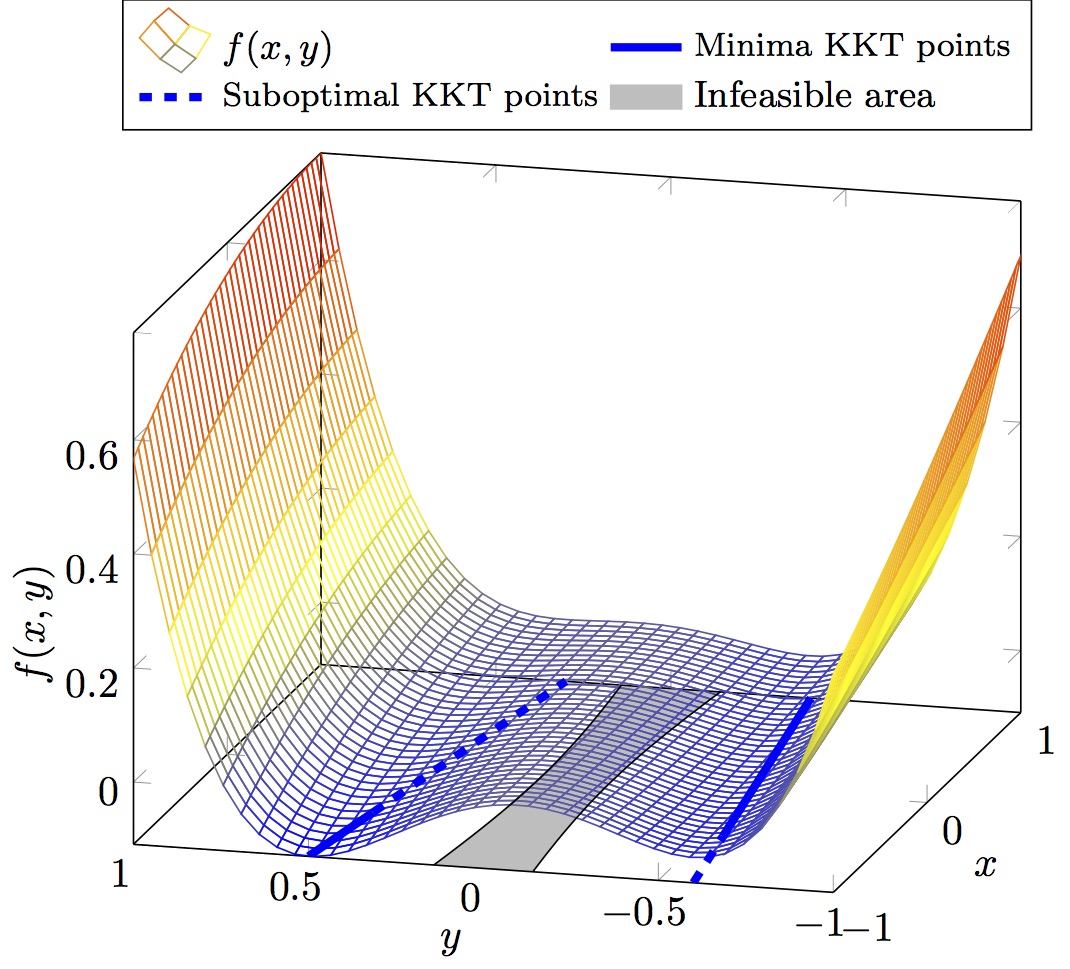
Optimal solution
| Objective values | Solution point(s) |
|---|---|
| F* = 0.210 | x* = -0.555 |
| f* = -0.069 | y* = 0.455 |
Illustration of the problem
| Outer Problem | Inner Problem |
|---|---|
 |
 |
Description in the AMPL format
var x >= -1, <= 1; # Outer variables
var y >= -1, <= 1; # Inner variables
var l{1..3} >= 0, <= 10; # Multipliers
minimize outer_obj: (x + 0.6)^2 + y^2;
subject to
# Inner objective
inner_obj: y^4 + (4/30)*(-x+1)*y^3 + (-0.02*x^2+0.16*x-0.4)*y^2 + (0.004*x^3-0.036*x^2+0.08*x)*y = 0;
# Inner constraints
inner_con: 0.01*(1+x^2) - y^2 <= 0;
# KKT conditions
stationarity: 0.004*x^3-0.036*x^2+0.08*x + (-0.04*x^2+0.32*x-0.8-2*l[3])*y + (-0.4*x+0.4)*y^2 + 4*y^3 - l[1] + l[2] = 0;
complementarity_1: l[1]*(-1 - y) = 0;
complementarity_2: l[2]*(y - 1) = 0;
complementarity_3: l[3]*(0.01*(1+x^2) - y^2) = 0;