BASBLib - A Library of Bilevel Test Problems

A growing collection of bilevel problems

mb_2007_03 : Linear-Quadratic bilevel problem from [Mitsos & Barton, 2007]

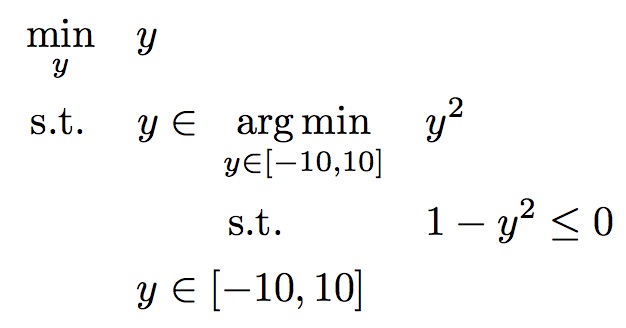
Optimal solution

Objective values Solution point(s)
F* = -1.000 y* = -1.000
f* = 1.000  

The feasible set for the inner problem is the union of [-10,-1] and [1,10] and its optimal solutions are y = +/-1. Thus unique optimal solution of the bilevel problem is y* = -1 with F* = -1 and f* = 1.

Illustration of the problem

Outer Problem Inner Problem

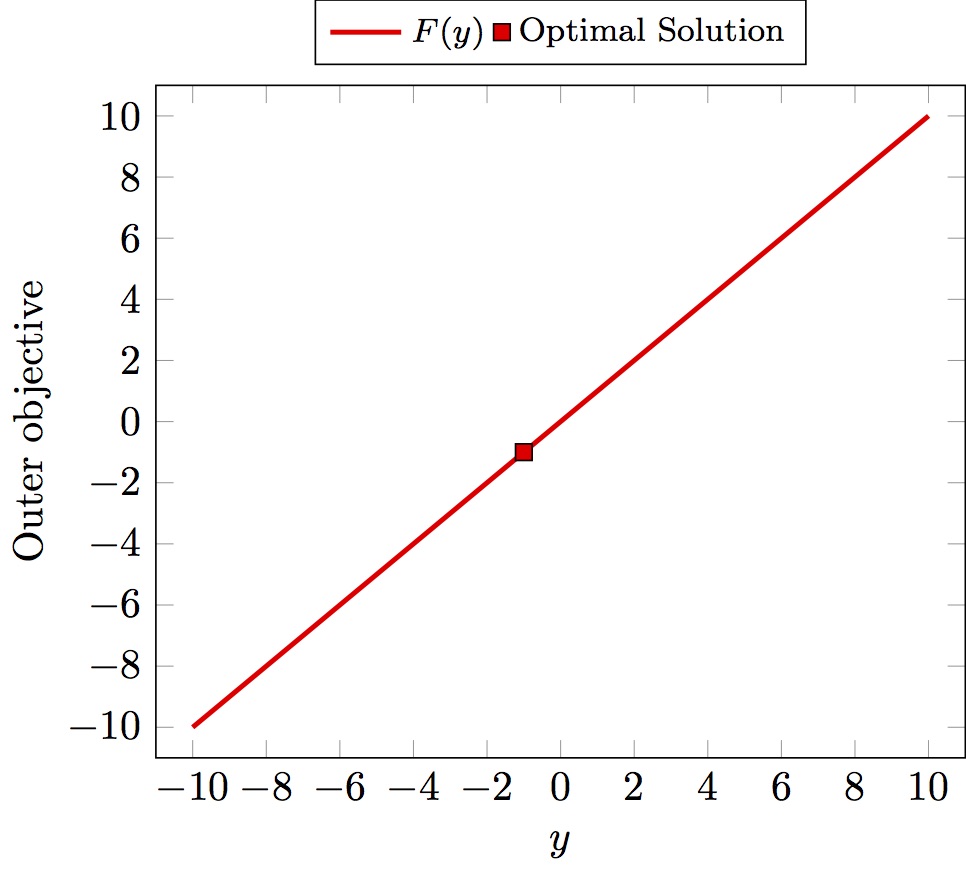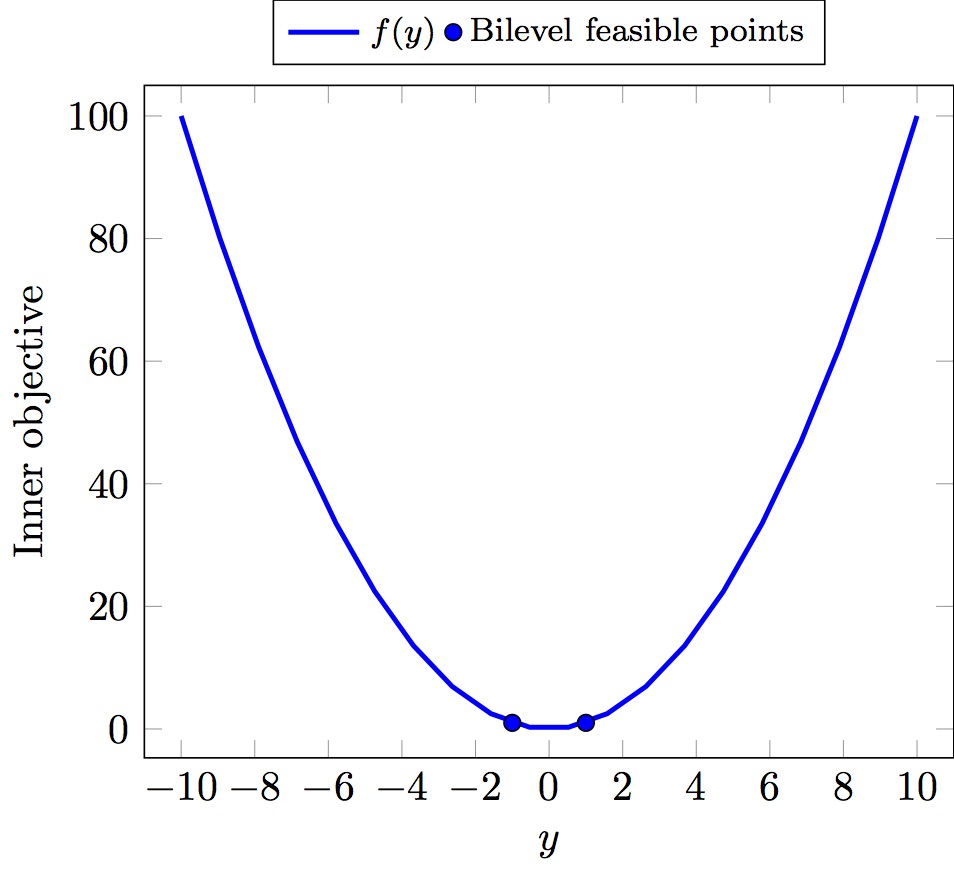Sources where this problem occurs

Original source:

Other sources:

Description in the AMPL format

var y >= -10, <= 10;      # Inner variable
var l{1..3} >= 0, <= 2;   # KKT Multipliers

minimize outer_obj: y;    # Outer objective

subject to
# Inner objective:
    inner_obj: y^2 = 0;
# Inner constraints
    inner_con: 1 - y^2 <= 0;
# KKT conditions
    stationarity: 2*y - 2*y*l[1] - l[2] + l[3] = 0;
    complementarity_1: l[1]*(1 - y^2) = 0;
    complementarity_2: l[2]*(-10 - y) = 0;
    complementarity_3: l[3]*(y - 10) = 0;

References